Новый алгоритм шифрования
Новый алгоритм шифрования
В рубрику "Защита информации" | К списку рубрик | К списку авторов | К списку публикаций
Новый алгоритм шифрования
Новый алгоритм шифрования, отличается от остальных алгоритмов тем, что вычисления производятся с определённой точностью, на основе тригонометрических функций. Особенность алгоритма состоит в том, что при увеличении точности вычислений период гаммирования может достигнуть сколь угодно большого значения. Наиболее близким к этому алгоритму является шифровальная машина "Enigma".
Содержание:
ВведениеКраткий пример описания простейшего алгоритма.
Статистические испытания.
Периодические функции используемые в данном алгоритме шифрования.
Сравнительный анализ разработанного алгоритма и уже существующих.
Доказательство бесконечности периода гаммирования.
Введение.
Поставленная цель достигается тем, что алгоритм в процессе вычисления работает с приближёнными значениями. Хотя при вычислениях получаются иррациональные числа, далее в последующих вычислениях используются только числовые промежутки в которые попали полученные иррациональные числа.
Краткий пример описания простейшего алгоритма.
Алгоритм реализован путем использования периодических функций типа y=cos x и уравнения "волны". Типа y=cos (x+Δx).
Сущность способа пояснена ниже:
Существует огромное количество периодических функций имеющих постоянную амплитуду которые определены и непрерывны на всем промежутке
 . График смотрите ниже.
. График смотрите ниже.
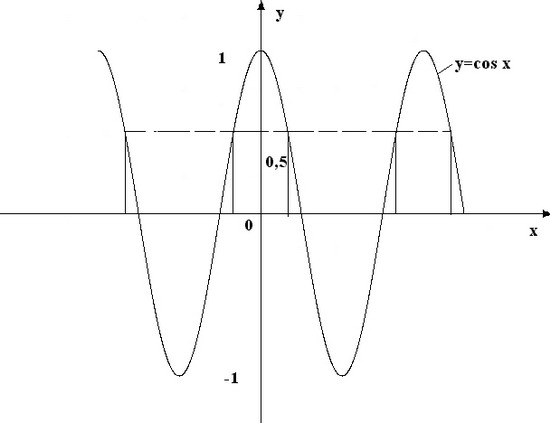
На графике представлена функция у = cos (x). Особенность периодической функции в том, что во первых её период выражен иррациональным числом, а во вторых например значению у = 0,5 соответствует бесконечное количество значений х. Т.е. при у = 0,5 х принимает значения
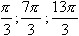 и т.д до бесконечности, как положительных так и отрицательных значений.
и т.д до бесконечности, как положительных так и отрицательных значений.
Применяя уравнение волны y=cos (x+N*Δx)
Где:
N – целое число в данном случае определяющее порядковый номер шифруемого символа (0-256)
Δx – приращение функции задаваемое в секретном ключе (любое число)
х – значение взятое из открытого текста. (0-256)
Получаем, что при у = 0,5 х может принимать любые значения от -∞ до +∞. Смотри ниже..
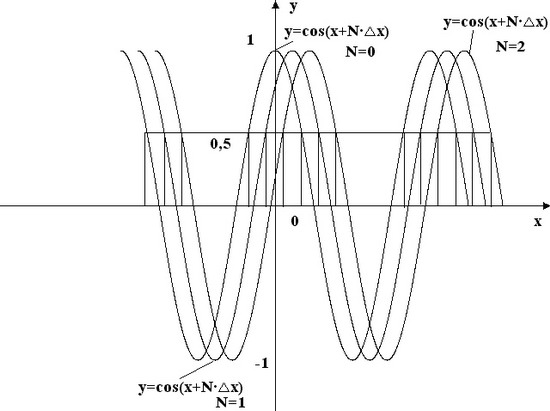
Предложенный способ осуществляется следующим образом. Создается компьютерная программа. По оси х расставляют и нумеруют те символы которые используются в открытом тексте, а по оси у те которые будут использованы в шифротексте. Зашифровывание идет по линейной функции у = х, которая перемещается по осям координат. Перемещение линейной функции у = х происходит по уравнению волны.
Пример реализации способа:
По координатной оси Х расставляются символы из открытого текста в любом порядке. Причём каждому символу соответствует свой порядковый номер например от 1 до 256. Всего используется в компьютере 256 символов. По оси Y расставляем символы используемые в шифротексте в любом таком же или другом порядке. Им так же присваиваются порядковые номера например от 1 до 256. Три линейные функции 1, 2, 3 описываются как: Y1, Y2, Y3.
Y1 = X + 256 * [cos(z + N*Δx)]+256
Y2 = X + 256 * [cos(z + N*Δx)]
Y3 = X + 256 * [cos(z + N*Δx)]-256
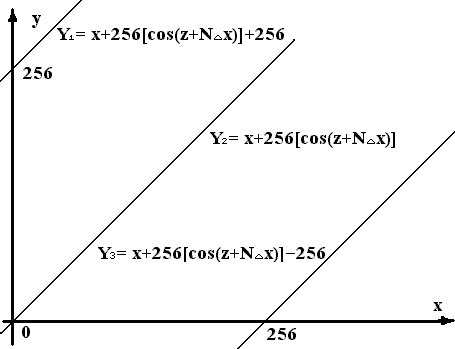
| Где: | Х – порядковый номер того символа из открытого теста; Z – любое число, например 0; Z 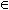 (-∞ до +∞) (-∞ до +∞)N - номер по счету шифруемого символа из открытого текста; Δx - любое число, например 32. Δx 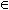 (-∞ до +∞) (-∞ до +∞)
|
Для примера зашифруем открытый текст состоящий из пяти букв А. ААААА – открытый текст.
В данном примере секретными является числа Δx и Z. Все остальные параметры не являются секретом. Кроме того количество секретных параметров можно сделать бесконечное множество.
Для примера порядок расстановки знаков по осям Х и У одинаковый. Например знак А занимает промежуток (0-1) по оси Х, знак Б-(1-2) В-(2-3)……..Я-(255-256). То же самое на оси У. Начинаем шифровать. Имея три формулы, подставляем значение 0,5 – середину промежутка (0-1) – буква А. Для буквы Б это значение соответствует 1,5 для В соответственно 2,5 для Я – 255,5
| Где: | Z = 0 (для удобства); N = 1 (т.к. шифруется первый по счету знак из открытого текста, потом 2,3,4,5); Δx = 32 |
Подставляем эти цифры в формулы.
Y1 = 0,5 + 256 * [cos(0 + 1*32)] + 256 = 437,6
Y2 = 0,5 + 256 * [cos(0 + 1*32)] = 217,6
Y3 = 0,5 + 256 * [cos(0 + 1*32)] - 256 = 38,39
Из трех значений Y1, Y2, Y3 выбираем Y2, так как оно попало в промежуток то 0 до 256. И округляем значение Y2 до большего целого Y2=218.
Шифруем второй знак открытого текста:
Y1 = 0,5 + 256 * [cos(0 + 2*32)] + 256 = 368,7
Y2 = 0,5 + 256 * [cos(0 + 2*32)] = 112,7
Y3 = 0,5 + 256 * [cos(0 + 2*32)] - 256 = -143,28
В шифротекст соответственно записываем Y2 = 113.
Соответственно получаем третий , четвертый и пятый знаки шифротекста:
Третий знак – 230 (N=3)
Четвертый знак – 99 (N=4)
Пятый знак – 16 (N=5)
В итоге из числового ряда 0,5; 0,5; 0,5; 0,5; 0,5 - открытый текст А А А А А получили числовой ряд 218; 113; 230; 99; 16 – шифротекст. Хочу отметить, цифры 218; 113; 230; 99; 16 получены путём округления иррациональных чисел. На самом деле вычисляются только до целого.
Для расшифровки применяют те же самые формулы
X1 = Y - 256 * [cos(z + N*Δx)] - 256
X2 = Y - 256 * [cos(z + N*Δx)]
X3 = Y - 256 * [cos(z + N*Δx)] + 256
Подставляя уже известные значения 218; 113; 230; 99; 16 получаем. Из каждого известного значения необходимо вычесть 0,5. Это делается для того, чтобы в формулу подставлялось значение из середины отрезка которому принадлежит данный знак. Т.е. в формулы по факту подставляются значения 217,5; 112,5; 229,5; 98,5; 15,5
| X1 = 217,5 - 256 * [cos(0 + 1*32)] - 256 = -255,6 | ||
| X2 = 217,5 - 256 * [cos(0 + 1*32)] = 0,4 | X = 0,4 | |
| X3 = 217,5 - 256 * [cos(0 + 1*32)] + 256 = 265,4 |
Подставляя следующие значения получаем остальные значения: 0,3; 0,7; 0,6; 0,56; все эти значения попали в промежуток (0-1) соответственно получили текст А А А А А.
Сам алгоритм шифрования имеет бесконечный период гаммирования. Это доказывается математически. Возьмём уже известную функцию Y = cos(x + Δx) само Δx может иметь значение от -∞ до +∞. Реально брать значение Δx в промежутке от 0 до -2π Если это значение не (-2π)/N где - любое целое число, то период гаммирования данной конкретной функции бесконечен. Сам алгоритм чем то напоминает шифровальную машину "Enigma". Вот если бы шифровальная машина "Enigma" в процессе шифрования вращалась не останавливаясь ни на мгновение с определённой секретной заданной скоростью и при этом имела очень тонкие контакты для снятия сигнала. То представленный алгоритм представляет эту математическую модель. Дело в том, что в процессе шифрования шифротекст представлен в виде иррациональных чисел. А в самом процессе шифрования участвуют промежутки в которые попадают эти иррациональные числа. Произвести аналитический взлом шифра возможно только точно зная само число, а оно иррационально то есть бесконечно и его не возможно вычислить и никто не вычисляет. Соответственно при расшифровании уже участвуют совершенно случайные числа, а не те которые получили в процессе шифрования, а середины числовых отрезков в которые попали иррациональные числа. При расшифровке опять получаются иррациональные числа которые не вычисляются в связи с бессмысленностью этой операции, а лишь те номера числовых отрезков в которые они попали.
Периодические функции используемые в данном алгоритме шифрования.
Вданном методе шифрования используются две периодические функции это SIN и COS. Если быть предельно конкретным фактически используется одна периодическая функция из перечисленных выше. Просто всегда возможно выразить одну функцию через другую.
Особенность этой функции (функций) состоит в том, что она непрерывна и определена на всем промежутке от минус бесконечности до плюс бесконечности на оси Х. А на оси У она принимает значения от –1 до 1, причем и на том и на другом промежутке она может принимать любые значения в этих промежутках. Над этими функциями возможно производить фактически любые математические действия. При этом функции принимают замысловатый вид в зависимости от произведенными над ними математическими действиями. Математическая задача состоит в том, чтобы функции имели как можно более широкий разброс в спектре частот содержащихся в функции. Кроме этого на качество шифрования очень сильно влияет биения содержащиеся в функциях. Представим одну из функций.
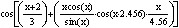 |
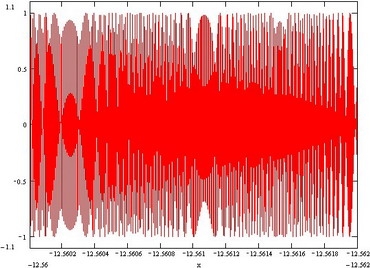 |
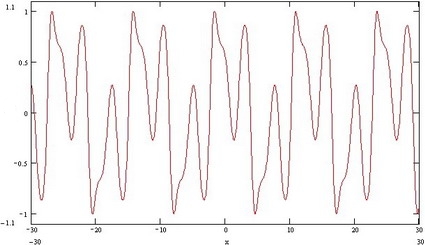
Как вы видите на графике функция имеет переменный спектр и переменную амплитуду. Рассмотрим эту же самую функцию но на более малом промежутке.
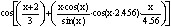 |
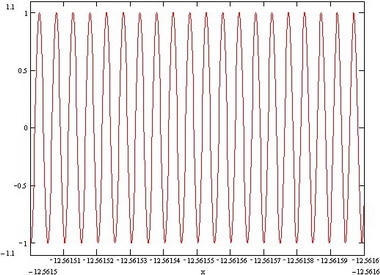 |
Как мы видим это синусоида. Частота синусоиды меняется на всем промежутке, и спектр частот можно регулировать.
Проделывая над функциями другие математические действия можно добиться биений функции. Как ярко выраженных так и слабо выраженных. Один из недостатков этих искусственных периодических функций состоит в том, что они симметричны относительно нуля, но это не влияет на качество шифрования, просто об этом нужно помнить. Можно искусственно сдвинуть всю функцию на фазу но это ничего не дает просто она становится симметрична относительно другой точки отсчета.
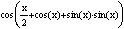 |
 |
Вообще те периодические функции которые используются в данном методе имеют одинаковый вид или проще мантиссу. Математическая задача ограничена тем, что проектируема периодическая функция должна иметь размах то –1 до 1, поэтому представленная мантисса имеет вид.
Х(У)
| Где: | Х – любая из двух периодических функций SIN COS. Y – сама формула шифрования. |
Вся математическая задача сводится к тому, чтобы составить такую периодическую функцию, которая отвечала некоторым данным.
ДАННЫЕ.
1 Функция должна иметь достаточно большой период повторения. Не путать с периодом функции. Это не расстояние между двумя точками на функции находящимися в одной фазе. Это расстояние между двумя точками после которой функция начинает полностью повторятся. Эта величина регулируемая и регулируется она двумя способами. Первый способ это использование соответствующих коэфицентов и периодических функций при составлении самой функции шифрования. А второй способ это зашифровывать один и тот же исходный текст несколько раз. И тот и другой способ можно использовать как вместе так и по отдельности.
2 Спектр частот используемых при составлении функции должен иметь максимальный разброс и все частоты должны по возможности более равномерно распределятся в шифрующей функции. Включая так же все гармоники и биения.
3 Размах функции шифрования должен достигать размеров от –1 до 1. При составлении некоторых функций эти колебания носят меньший размах причем не на всем протяжении функции а на ее частях. В этом случае ваша шифровка будет иметь нормальный закон распределения, что крайне не желательно. Полагаясь на эту информацию можно уже сделать вывод о расстановке символов на оси Х, и даже возможно сделать вывод о примерном содержании текста. Кроме этого различные тексты носят различный символьный спектр. Это нужно учитывать, но при работе над серьезной программой, зная, что взлом будут производить например государственные структуры. Кроме этого имеет смысл опасаться специализированных компьютеров оборудованных специальными процессорами которые отличаются не только быстродействием, но и имеют перестраиваемый процессор.
Сравнительный анализ разработанного алгоритма и уже существующих.
Сравнительная таблица.
| Сравниваемые параметры. | Общеизвестный способ. DES | Предлагаемый способ. | Идеальное распределение |
| Тип зашифрованного текста. | 6 Мб текста состоящих из начального байта при побитовом разложении 0. | 6 Мб текста состоящих из начального байта при побитовом разложении 0. | 6 Мб текста состоящих из начального байта при побитовом разложении 0. |
| Закон распределения. (Спектр) | Нормальный. | Равномерный. | Равномерный. |
| Количество сочетаний знаков встречаемых в шифровке. | 25188 | 65536 | 65536 |
| Количество повторений встречающихся в тексте. | 2 - 106; | 2 - 85; | 2 - 96; |
| Увеличение объема зашифрованного текста. | На 8 байт | На 2 байта | Нет увеличения |
| Время шифрования. | 6 минут 20 секунд | 25 секунд | _____ |
| Общее количество 0 и 1 в шифровке. | 1 - 25349346; 0 - 25232158; % - 0.231682%. |
1 - 25159905; 0 - 25171743; % - 0.023520%. |
1 - 25168277; 0 - 25163435; % - 0.009620%. |
1.Тип шифруемого текста.
Для шифрования выбран исходный текст размерностью 6 Мб. Весь текст состоит из одного единственного знака, в кодовой таблице 866 – MS - DOS это знак пробела. Этот знак выбран не случайно. При побитовом разложении этого знака все биты имеют значение 0. Текст такого типа зашифровать очень трудно. Кроме этого для шифрования выбран поточный выбор опять же не случаен. Поточные методы шифрования являются более слабыми по сравнению с блочными методами поэтому выбраны именно они.
2.Закон распределения.
В шифровке подсчитывается количество каждого используемого знака, результаты выводятся в виде графика. Кроме этого производятся исследования распределения в исследуемом методе шифрования относительно оси Х для решения вопроса по какому закону распределения распределяются знаки на оси Х. Если закон распределения равномерный с малыми амплитудными колебаниями это является наилучшим показанием. Ниже приведены три графика спектра распределения. График предлагаемой системы шифрования, системы DES, и идеального "белого шума".
График системы DES шифрования.
По оси Х расставлены те знаки которые встречаются в шифровке (встречаются все знаки).
По оси У количество выпавших знаков. В данном графике знаки не отсортированы и расположены на оси Х в том же порядке что и в программе шифрования.
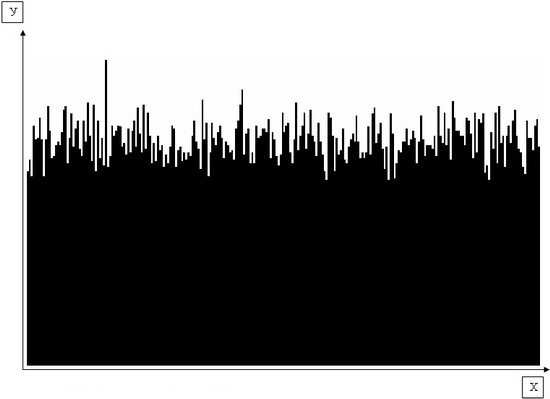
График 1 принадлежащий системе DES.
График идеального распределения.

График 3
График распределения предложенного способа.
График 4

3.Количество сочетаний.
В шифротексте подсчитывается количество всех возможных сочетаний используемых знаков. Для этого происходит перебор и подсчет всех существующих двойных сочетаний знаков. В шифровке используется 256 знаков. Пронумеруем их 1,2,3,4…….256. Происходит перебор и подсчет всех возможных двойных сочетаний этих знаков. Начиная с первого знака, сочетания. (1,1),(1,2),(1,3),(1,4)……(1,256). После этого проводится инвертирование сочетаний начиная со второго сочетания (2,1),(3,1),(4,1)……(256,1). Следующим перебором является (2,2),(2,3),(2,4),(2,5)……(2,256). С последующим инвертированием начиная со второго знака. И так далее до сочетания (256,256). Инвертирование которого уже не производится. Происходит подсчет четных и нечетных сочетаний. То есть весь перебор происходит сначала с первого знака , потом первый знак отбрасывается и происходит тот же перебор но уже со второго знака. После этого происходит подсчет всех перебранных сочетаний и результаты выводятся в виде таблицы. Максимальное количество сочетаний и равномерный закон их распределений является наилучшим показателем.
Ниже приведены так же три графика. Для системы DES. Для идеальной системы, и для предложенной системы.
По оси Х показано количество полученных сочетаний а по оси У количество каждого сочетания в шифровке.

Система распределения для DES.

График 7
Как видим на графике используется только 38% возможных сочетаний и они имеют ступенчатую кривую.
Максимум сочетаний по оси У составляет 1005.
Идеальная система шифрования.

График 8
В данной системе происходит перебор всех возможных сочетаний. Максимальный размах по оси У составляет 141 знак.
График распределения предложенной системы.

График 9
Как видно из графика используются все возможные сочетания знаков. Максимальный размах по оси У составляет 209.
Ниже приведён исходный текст программы по которой проводилось непосредственно шифрование. Прогамма написана на С++.
//---------------------------------------------------------------------------
#include <stdio.h>
#include <Gizur\dsfile.h>
#include <conio.h>
#include <math.h>
#include <fastmath.h>
#include <time.h>
#include <stdlib.h>
#pragma hdrstop
//---------------------------------------------------------------------------
#pragma argsused
//---------------------------------------------------------------------------
double __fastcall TrueCos(double Angle)
{
return cos(Angle * 3.14159 / 180);
}
//---------------------------------------------------------------------------
double __fastcall TrueSin(double Angle)
{
return sin(Angle * 3.14159 / 180);
}
//---------------------------------------------------------------------------
void EncodeFile(char *InputFilename, char *OutputFilename)
{
__File *InputFile = new __File(InputFilename, O_RDONLY | O_BINARY);
__File *OutputFile = new __File(OutputFilename, O_WRONLY | O_BINARY |
O_CREAT | O_TRUNC, S_IWRITE);
unsigned char Buffer[8193], CurrentByte, Current = 0;
unsigned int WasRead = 1, Position = 0;
double Result;
unsigned char ByX[256], ByY[256];
unsigned char AntiX[256], AntiY[256];
for (int Symbol = 0; Symbol < 256; Symbol++)
{
ByX[Symbol] = Current;
AntiX[Current] = Symbol;
Current = (Current + 2) * 13 - 1;
};
Current = 2;
for (int Symbol = 0; Symbol < 256; Symbol++)
{
ByY[Symbol] = Current;
AntiY[Current] = Symbol;
Current = (Current + 2) * 13 - 1;
};
randomize();
unsigned char LastByte = random(256);
double Sins[256], Coses[256], CurSin, LastSin;
for (int Value = 0; Value < 256; Value++)
{
Sins[Value] = sin(Value);
Coses[Value] = cos(Value);
};
printf("Table was created.\n");
long StartTime = time(NULL);
while (WasRead)
{
WasRead = InputFile->Read(Buffer, 8192);
printf(".");
for (int Symbol = 0; Symbol < WasRead; Symbol++)
{
for (int Times = 3; Times; Times--)
{
CurrentByte = ByX[Buffer[Symbol]];
LastSin = Sins[LastByte];
CurSin = sin(CurrentByte);
Result = 256 * _fm_cos((0.406 * CurrentByte + _fm_cos(CurrentByte +
LastSin) + 2.43 * CurSin * CurSin) / (5 * Coses[LastByte]
+ 5.05) + 2.18 * Position * LastSin) + Position;
Result += (Result > 0) ? 0.5 : -0.5;
LastByte = CurrentByte;
CurrentByte = Result;
Buffer[Symbol] = AntiY[CurrentByte];
}
Position++;
}
OutputFile->Write(Buffer, WasRead);
};
delete OutputFile;
delete InputFile;
printf("\n\r");
int CurTime = time(NULL) - StartTime;
printf("%d\n\r", CurTime);
}
//---------------------------------------------------------------------------
int main(int argc, char* argv[])
{
printf("Encoder v1.0.0.1\n\r");
if (argc == 3)
EncodeFile(argv[1], argv[2]);
printf("Press any key to continue.\n\r");
getch();
return 0;
}
//---------------------------------------------------------------------------
Программа специально написана для прохождения тестов.
Из всего вышесказанного можно сделать выводы, что предложенный алгоритм шифрования является лучшим чем DES/
Доказательство бесконечности периода гаммирования.
Представленный алгоритм обладает бесконечным периодом гаммирования. Этот факт доказывается следующим образом.
Если взять элементарную периодическую функцию с уравнением волны типа
y = cos (x + Δx)
То в этом случае период функции равен 2π, а период гаммирования равен n1 раз при условии Δx * n1 = 2π * n2 где n1, n2 целые числа. Это условие выполнимо только при условии что, nΔx = n2π где n -любые целые числа не равные между собой. Это возможно только в том случае если Δx кратно 2π.
Внутри современного процессора не существует числа 2π. Всякий раз это значение вычисляется по следующему алгоритму.
Зная например ряд функции cos.
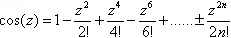
Для удобства пусть z = π / 2 тогда в этом случае ряд равен 0.
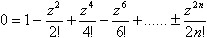
Исходя из этого появляется возможность с любой точностью вычислить число π, что и происходит в процессоре.
В 1949 г. Число пи было вычислено с 2000 знаков, а в 1957 г. с точностью 10 000 знаков. Надо отметить что все цифры в числе пи встречаются одинаковое число раз, но никакой закономерности в чередовании цифр обнаружить не удалось, они следуют одна за другой совершенно беспорядочно.
Во время работы алгоритма внутри машины вычисление числа π происходит всякий раз заново и всякий раз с определённой точностью необходимой на конкретный шифруемый знак. То есть можно сказать, что время потраченное на шифрование каждого знака различно и зависит от длины числа π. Теоретически возможен вариант, что машина не сможет вычислить число π с необходимой точностью в установленных временных рамках или зарегистрированной длины числа π. В этом случае произойдёт сбой алгоритма и он не выполнится. Вероятность этого события стремится к 0.
Если рассматривать сам механизм алгоритма более подробно, то увидите. В алгоритме используется иррациональное число подобное π, которое так же вычисляется с использованием рядов.
Теоретически сам процесс шифрования несколько сложен и проводится путём подстановки по некоторым причинам.
1)Возможно с использованием ряда сгенерировать любое иррациональное число подобное π и логическим И сложить с исходным текстом. В этом случае при вычислении каждого нового члена ряда по времени происходит всё дольше и растёт с геометрической прогрессией.
2) При подстановке иррациональное число практически генерируется только до определённой точности, а теоретически может идти вычисление бесконечно долго.
Сизов Владимир Петрович, инженер
Опубликовано: Сайт ITSec.Ru-2007
Статьи про теме
Copyright © 2018-2025, ООО "ГРОТЕК"








